Gear is a widely used spare part in life, whether it is aviation, freighter, automobile, etc., it will be used. However, when the gear is designed and processed, its number of teeth is required. Some people say that if it is less than 17 teeth, it cannot be rotated, and some people say that it is wrong. There are many gears below 17 teeth. In fact, these statements are correct, do the gold powders know why? Welcome to leave a message for discussion.
Why is the number of teeth 17?
Then why 17? instead of other numbers? As for 17, this starts with the processing method of the gear, as shown in the figure below, a widely used method is to use a hob to cut.
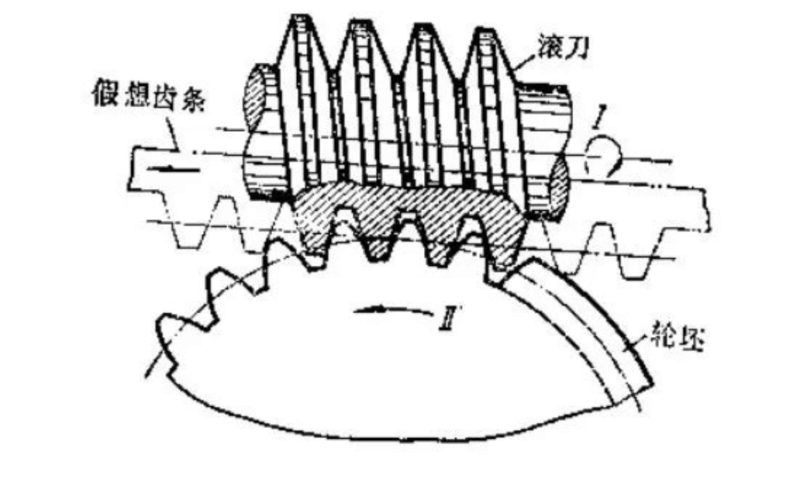
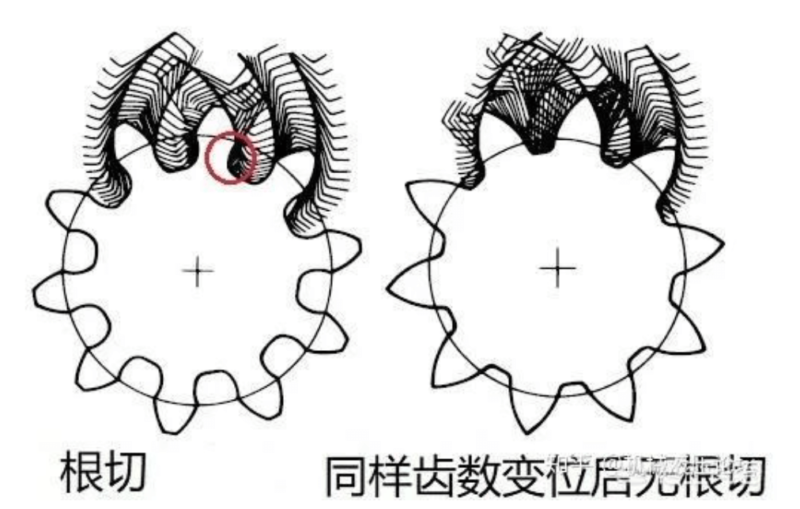
When gears are manufactured in this way, when the number of teeth is small, the undercut phenomenon will occur, which will affect the strength of the manufactured gears. What is root cutting is that the root is cut. . . Pay attention to the red box in the figure:
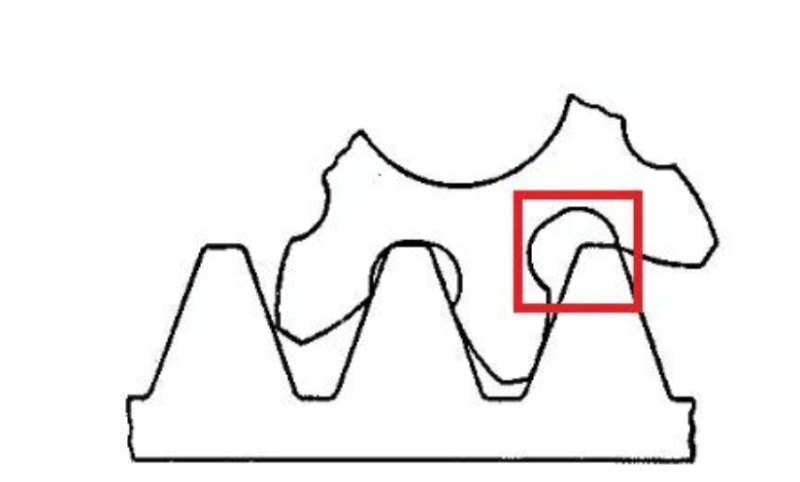
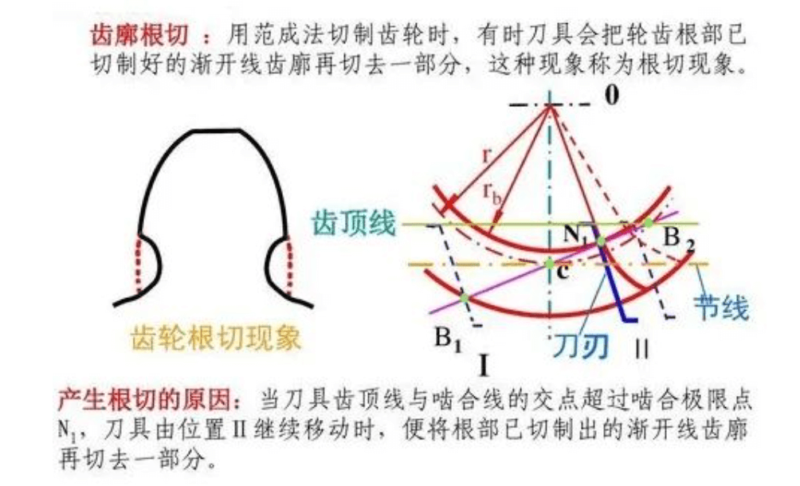
When the intersection of the tooth top and the meshing line of the gear exceeds the limit meshing point of the gear being cut, a part of the involute tooth profile of the tooth root of the gear being cut is cut off. This phenomenon is called undercutting.
So when can undercutting be avoided? The answer is this 17 (addition height coefficient 1, when the pressure angle is 20 degrees).First of all, the reason that the gear can rotate is because a good transmission relationship must be formed between the upper gear and the lower gear. Only when the connection between the two is in place, can its operation be a smooth relationship. Take the involute gear as an example, only when the two gears are meshed well can it play its role. Specifically, it is divided into two types: spur gears and helical gears.The coefficient of the tooth top height of a standard spur gear is 1, the coefficient of the tooth heel height is 1.25, and the degree of its pressure angle should reach 20 degrees. When the gear is processed, if the tooth germ and the tool are like two gears Same.If the number of teeth of the embryo is less than a certain value, a part of the root of the tooth root will be dug out, which is called undercut. If the undercut is too small, it will affect the strength and stability of the gear. The 17 mentioned here are for gears. If we don’t talk about the working efficiency of gears, it will work and run no matter how many teeth there are.In addition, 17 is a prime number, which means that the number of coincidences of a certain tooth of a gear and a certain number of other gears is the least under a certain number of turns, and it will not be at this point for a long time when the force is applied. Gears are precision instruments. Although there will be errors on each gear, the probability of 17 wheel shaft wear is too great, so if it is 17, it will be fine to move for a while in the short term, but not in the long term.But here comes the problem! There are still many gears with less than 17 teeth on the market. They still turn well. There are pictures and truths!

Some netizens pointed out that, in fact, if you change the processing method, it is possible to manufacture standard involute gears with less than 17 teeth. Of course, such gears are also easy to get stuck in use (due to the interference of the gears, the picture cannot be found, please make up your mind), so it really can’t turn. There are many corresponding solutions. The displacement gear is the most commonly used one (in layman’s terms, the tool is moved a little when cutting), and there can also be helical gears, cycloid gears, and so on. And there are pan-cycloid gears.
Another netizen’s point of view: Everyone seems to believe in books too much. I don’t know how many people have thoroughly studied gears at work. In the first lesson of mechanical principles, there is no root for involute spur gears with more than 17 teeth. The derivation of the cut is based on the fact that the top fillet R of the rake face of the rack tool for machining the gear is 0. In fact, how can there be no R angle in the tool in industrial production? (The heat treatment of the tool without the R angle means that the stress concentration of the sharp part is easy to crack, and it is easy to wear or crack during use.) And even if the tool does not have an R angle undercut, the maximum number of teeth may not be 17 teeth, so 17 teeth are used as the undercut condition. It’s actually up for debate! Let’s take a look at the pictures above.
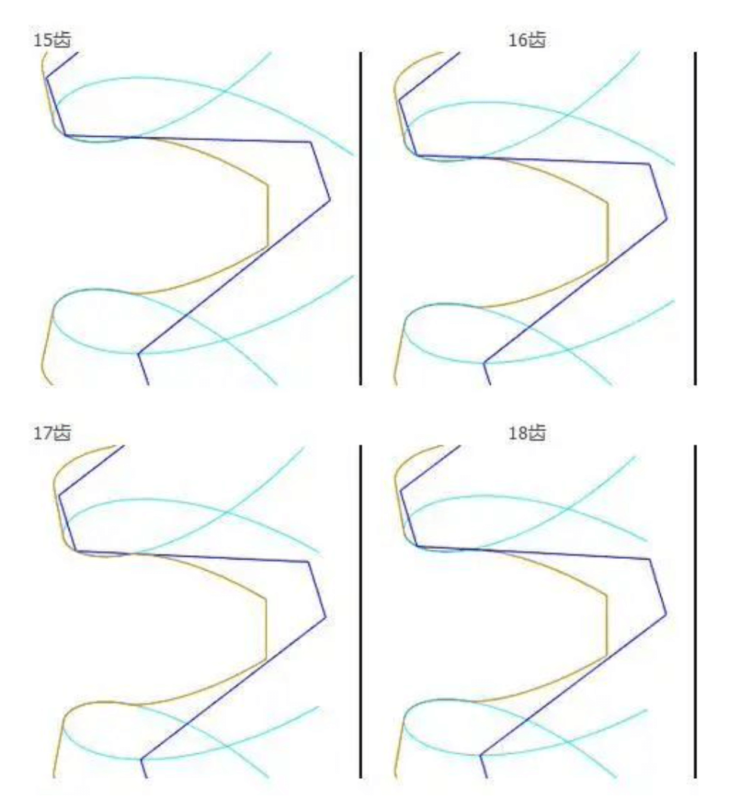
It can be seen from the figure that there is no obvious change in the tooth root transition curve from 15 teeth to 18 teeth when the tool with the R angle at the top of the rake face is 0 to process the gear, so why is the 17 tooth starting with an involute straight tooth? What about the number of teeth that undercut?

This picture must have been drawn by students majoring in mechanical engineering with the gear fan Chengyi. It can be seen that the size of the R angle of the tool affects the undercut of the gear.
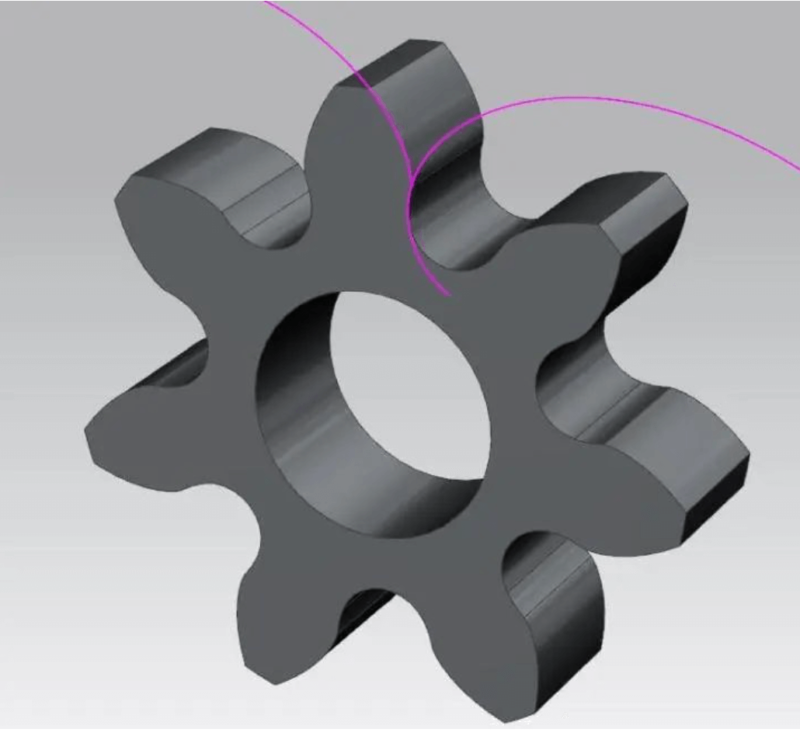
The equidistant curve of the purple extension epicycloid of the tooth root part in the above figure is the tooth profile after the tooth root is undercut. To what extent does the undercut of the tooth root part of a gear affect the use? This is determined by the relative movement of the tooth top of the other gear and the strength reserve of the tooth root of the gear. If the tooth top of the paired gear does not mesh with the undercut part, the two gears can rotate normally. (Note: Undercut Part of it is a non-involute tooth profile, an involute tooth profile and a non-involute tooth profile meshing are usually unconjugated in the case of non-specific design, that is, to interfere).
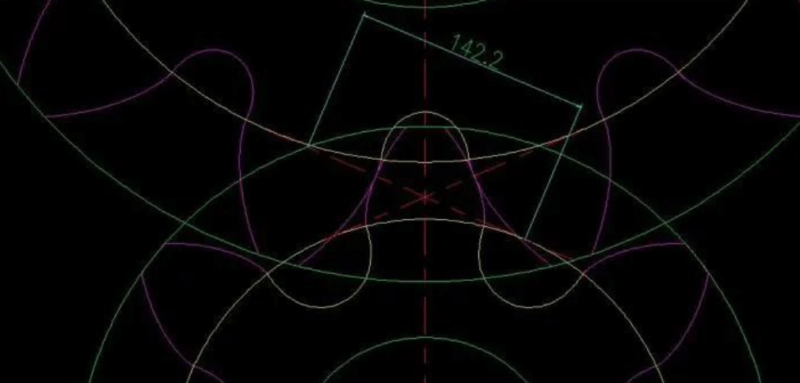
It can be seen from this picture that the meshing line of the two gears has just wiped the largest diameter circle opposite to the transition curve of the two gears (Note: the purple part is the involute tooth profile, the yellow part is the undercut part, the meshing line It is impossible to enter below the base circle, because it is impossible to have an involute below the base circle, and the meshing point of the two gears at any position is on this line), that is, the two gears can mesh normally just now. It is not allowed in engineering, the length of the meshing line is 142.2, this value / base section = coincidence degree.
Someone else said: First of all, this question is wrong, the gear less than 17 teeth will not affect the use (the description of this point in the first answer is wrong, the three conditions for the correct meshing of the gear have nothing to do with the number of teeth), but 17 teeth in a certain In some specific cases, there will be inconvenient processing. Here is more to add some related knowledge about gears.
Let’s start with the involute, which is the most widely used type of gear tooth profile. So why involute? What is the difference between this line and a straight line and an arc? It is an involute as shown in the figure below (here there is only an involute of half a tooth).
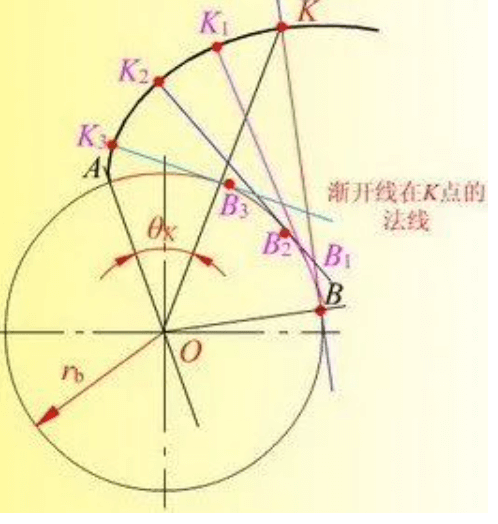
In one sentence, an involute is a trajectory traversed by a fixed point assuming a straight line and its previous fixed point when the straight line rolls along a circle. Its benefits are obvious when two involutes mesh with each other, as shown below.
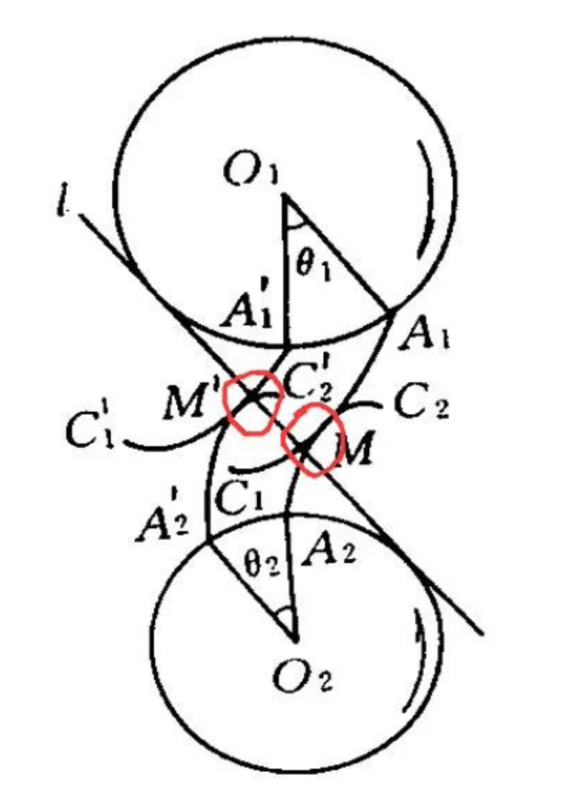
When the two wheels rotate, the acting direction of the force at the contact point (such as M , M’ ) is always on the same straight line, and this straight line is perpendicular to the two involute-shaped contact surfaces (tangent surfaces). There will be no “slip” and “friction” between them, which objectively reduces the friction of gear meshing, which not only improves efficiency, but also prolongs the life of gears.
Of course, as the most widely used form of tooth profile, involute is not our only choice.
Speaking of “root cutting”, as engineers, we not only need to consider whether the theoretical level is feasible, whether the effect is good or not, but more importantly, we need to find a way to present the theoretical things, which involves material selection, manufacturing, precision, testing, etc. and so on.
The commonly used processing methods of gears are generally divided into forming method and Fan Cheng method. The forming method is to directly cut out the tooth shape by manufacturing a tool corresponding to the shape of the gap between the teeth. This generally includes milling cutters, butterfly grinding wheels, etc.; Fan Cheng method compares Complex, we can understand that two gears are meshing, one of which is very hard (tool), and the other is still in the embryonic state. The process of meshing is gradually moving from far away to a normal meshing state. During this process Medium cutting produces new gears, and those who are interested can learn from “Mechanical Principles”.
Fan Cheng method is widely used, but when the number of gear teeth is small, the intersection of the tooth top line and the meshing line of the tool will exceed the meshing limit point of the gear to be cut, and the root of the gear to be processed will be crossed. Removal, since the undercut part exceeds the meshing limit point, it does not affect the normal meshing of the gears, but the disadvantage is that it weakens the strength of the gear teeth. When such gears are used in heavy-duty occasions such as gearboxes, The gear teeth are prone to breakage, as shown in the figure after the normal machining of the 2-mode 8-tooth gear (with undercut).
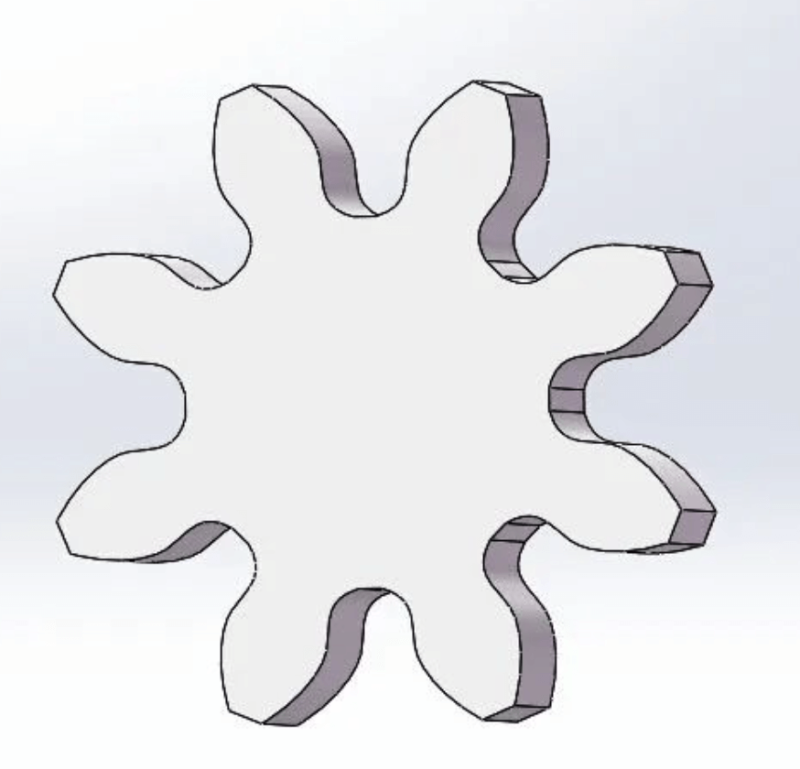
And 17 is the limit number of teeth calculated in the case of my country’s gear standard. Gears with a number of teeth less than 17 will appear “undercutting phenomenon” when using the Fan Cheng method to process normally. At this time, the processing method should be adjusted, such as displacement, as shown in the figure 2-mode 8-tooth gear for displacement processing (small undercut).

Of course, many of the contents described here are not comprehensive. There are many more interesting parts in machinery, and there are more problems in manufacturing these parts in engineering. Interested gold powder may wish to pay more attention.
Conclusion: The 17 teeth come from the processing method, and it also depends on the processing method. If the processing method of the gear is replaced or improved, such as forming method and displacement processing (here, the spur gear is specifically referred to), there will be no undercutting phenomenon. There is no limit to the number of 17 teeth.
In addition, from this question and its answer, we can see a feature of the mechanical discipline – a high degree of integration of theory and practice.
Netizen’s point of view: First of all, it is incorrect to say that gears with less than 17 teeth cannot rotate. Let us briefly introduce how the number of 17 teeth came from.
Gear refers to a mechanical element that continuously meshes with gears on the rim to transmit motion and power. The gear tooth profile has involute, arc, etc., and involute gears are widely used.
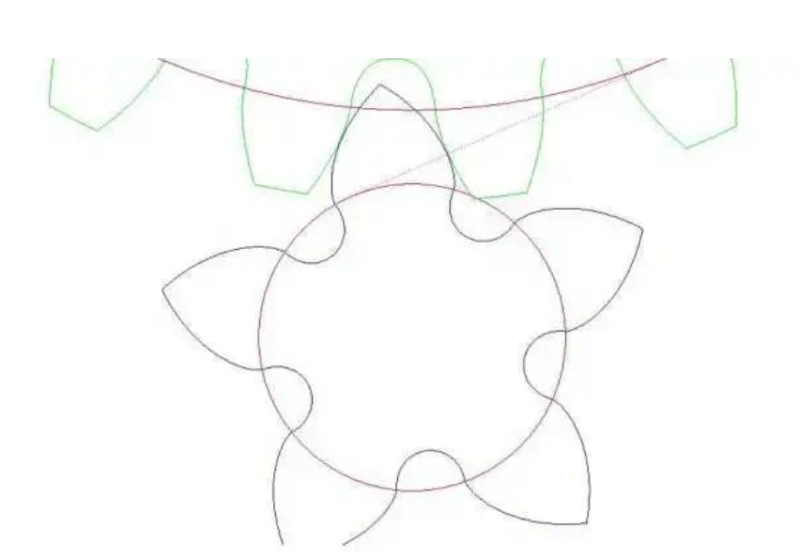
Involute gears are divided into spur gears/helical gears, etc. For standard spur gears, the addendum height coefficient is 1, the tooth root height coefficient is 1.25, and the pressure angle is 20°. When machining gears, the Fan Cheng method is generally used, that is, the movement of the tool and the gear blank during machining is like a pair of gears meshing with each other. For standard gear processing, if the number of teeth is less than a certain value, a part of the involute contour at the root of the gear blank will be dug out, which is called undercut, as shown on the left below, the undercut will seriously affect the strength and transmission of the gear The stability of the , the minimum value of this no undercut is 2*1/sin (20) ^ 2 (1 is the addendum height coefficient, 20 is the pressure angle).
The 17 teeth here are for standard spur gears. We have many ways to avoid undercuts, such as gear displacement, that is, the tool is far away from or close to the center of rotation of the wheel blank. In order to avoid undercuts, we need to choose Away from the center of contour rotation, as shown on the right below, is the complete involute contour line coming out again?
After the gear is displaced, the gear can be rotated without being affected, and the 5-tooth gear can also be rotated by appropriate displacement.
In fact, helical gears can also avoid gear undercuts, or reduce the minimum number of teeth at which undercuts occur.
The number 17 is calculated. It is not that a few 17 gears can’t turn, but if there are less than 17 teeth, it is easy to cut off a part of the root of the gear with the machined spaced line during gear processing, that is, undercut, resulting in the weakening of the strength of the gear. As for how to calculate, it is completely a mathematical problem. Referring to the above formula, the kneading angle a = 20 degrees, and the minimum number of teeth without undercutting is 17.
Netizen’s point of view: Whether the number of teeth of the gear can be less than 17 is a question worthy of consideration. For a standard gear, the number of teeth can’t be less than 17, why? Because when the number of teeth is less than 17, the gear will be undercut.
The so-called undercut means that when cutting the teeth with the Fancheng method, under certain conditions, the tooth top of the tool cuts too much into the root of the gear tooth, and the involute tooth profile of the tooth root is cut off.
Fan Chengfa and Undercut
Fan Chengfa
The Fan Cheng method (or the generation method ) is a method of machining gears using the geometric enveloping principle. After the involute tooth profile of the two gears and the angular velocity w 1 of the driving wheel are given, the angular velocity w 2 of the driven wheel can be obtained through the meshing of the two tooth profiles , and i 12 = w 1 / w 2 = constant value. Because in the meshing of the two tooth profiles, the two pitch circles are purely rolling, and in the process of pure rolling of pitch circle 1 on pitch circle 2, the tooth profile of gear 1 will occupy a series of relative positions to gear 2, and the relative position of this series of relative positions will be The envelope is the tooth profile of the gear 2, that is, when the two pitch circles are purely rolling, the two involute tooth profiles can be regarded as mutual envelopes.
undercutting phenomenon
The reason for the undercut: when the intersection of the tool tooth top line and the meshing line exceeds the meshing limit point N1, and the tool continues to move from position II, the involute tooth profile that has been cut at the root is cut off again.
Consequences of undercutting: gears with severe undercuts, on the one hand, weaken the bending strength of the gear teeth; The reason for the undercut: When the intersection of the tool tooth top line and the meshing line exceeds the meshing limit point N1, and the tool continues to move from the position II, the involute tooth profile that has been cut at the root is cut off again.
For non-standard gears, less than 17 teeth is fine.










